How to Create ZKP to de-link Deposit and Withdrawal on EVM Chains

What is Zero Knowledge Proof (ZKP)

It is a cryptographic method where one party (the prover) can prove to another party (the verifier) that a statement is true without revealing any additional information beyond the fact that the statement is true. For example, it can prove knowledge of a secret without disclosing the secret itself. EVM chains examples are Ethereum, Binance, Polygon, Arbitrum, Optimism, Base etal.

How to use ZKP to hide transaction, disconnect, de-link deposit and withdrawal on EVM chains

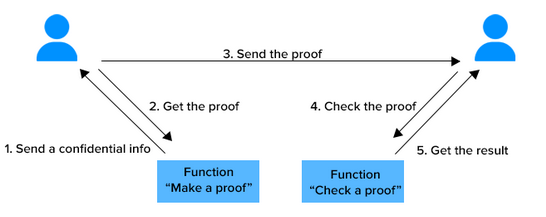
You may be asking what is the purpose of ZKP. Well, as you know, every transaction is visible on the blockchain to the public; assuming your wallet is known or popular, anyone can trace or monitor as you receive deposit and also transfer out crypto or tokens to other wallet. But with ZKP, you can de-link or disconnect your wallet transactions by separating deposit from withdrawal. This is the similar technology that platform like tornado cash uses to de-link deposit from withdrawal onchain. The below briefly describe the workflow:

• “Person G” Deposits Crypto Coin or Token eg Eth, Bnb to the Contract with some unique Identifier on 19 July, 2025 10am for example.
• For anyone eg. “Person K” or same “Person G” to withdraw later in the future, they use ZKP to submit a proof without revealing the secret or unique identifer that shows to the verifier that they know a secret. The withdrawal can be made at any future time after the successful deposit, can be days, weeks, months, minutes, hours as they want to.

The above is the simple overall description of how it works. I will share below some code that ensure this happens. Circom is used to write the ZKP logic verifier which is later used to generate the Verifier.sol contract code:

pragma circom 2.0.0;

include "CommitmentHasher.circom";
//include "MerkleTreeChecker.circom";

template Private() {
    signal input nullifier;
    signal input secret;
    signal input receiver;
    
    //signal input relayer; //address that push the transaction
    //signal input contractAddress;//address that host or controls the deposit.
    
    signal output nullifierHash; //to check double spending.
    
    component commitmentHasher = CommitmentHasher();

    commitmentHasher.nullifier <== nullifier;
    commitmentHasher.secret <== secret;

    nullifierHash <== commitmentHasher.nullifierHash;

    //d_commitment <== commitmentHasher.commitment;

    // Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof
    // Most likely it is not required, but it's better to stay on the safe side and it only takes 2 constraints
    // Squares are used to prevent optimizer from removing those constraints

    signal receiverSquare;

    receiverSquare <== receiver * receiver;
}

/*contractAddress amount*/
//public input 
component main{public [ receiver ]} = Private();

the Solidity code:

// SPDX-License-Identifier: GPL-3.0
/*
    Copyright 2021 0KIMS association.

    This file is generated with [snarkJS](https://github.com/iden3/snarkjs).

    snarkJS is a free software: you can redistribute it and/or modify it
    under the terms of the GNU General Public License as published by
    the Free Software Foundation, either version 3 of the License, or
    (at your option) any later version.

    snarkJS is distributed in the hope that it will be useful, but WITHOUT
    ANY WARRANTY; without even the implied warranty of MERCHANTABILITY
    or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public
    License for more details.

    You should have received a copy of the GNU General Public License
    along with snarkJS. If not, see <https://www.gnu.org/licenses/>.
*/

pragma solidity >=0.7.0 <0.9.0;

contract Groth16Verifier {
    // Scalar field size
    uint256 constant r    = 21888242871839275222246405745257275088548364400416034343698204186575808495617;
    // Base field size
    uint256 constant q   = 21888242871839275222246405745257275088696311157297823662689037894645226208583;

    // Verification Key data
    uint256 constant alphax  = 20491192805390485299153009773594534940189261866228447918068658471970481763042;
    uint256 constant alphay  = 9383485363053290200918347156157836566562967994039712273449902621266178545958;
    uint256 constant betax1  = 4252822878758300859123897981450591353533073413197771768651442665752259397132;
    uint256 constant betax2  = 6375614351688725206403948262868962793625744043794305715222011528459656738731;
    uint256 constant betay1  = 21847035105528745403288232691147584728191162732299865338377159692350059136679;
    uint256 constant betay2  = 10505242626370262277552901082094356697409835680220590971873171140371331206856;
    uint256 constant gammax1 = 11559732032986387107991004021392285783925812861821192530917403151452391805634;
    uint256 constant gammax2 = 10857046999023057135944570762232829481370756359578518086990519993285655852781;
    uint256 constant gammay1 = 4082367875863433681332203403145435568316851327593401208105741076214120093531;
    uint256 constant gammay2 = 8495653923123431417604973247489272438418190587263600148770280649306958101930;
    uint256 constant deltax1 = 486013274891713649403578868029229898276528189263461313807316370848035074657;
    uint256 constant deltax2 = 18546248312776679677211199480938669833952401325023235924944922036599014476436;
    uint256 constant deltay1 = 15986653496605210869470164083261109372255314436009451528249871163252308925673;
    uint256 constant deltay2 = 14901565306515110999279778193504803224130708883248808381099651191452604992188;

    
    uint256 constant IC0x = 15744513443685431653489977124559316775589144373101905215540098362271682264636;
    uint256 constant IC0y = 6181230803245730221322895786403215897209999458320708362064389956730848313282;
    
    uint256 constant IC1x = 5670333109040999605532207042029676573423810467263412828429337280223735635438;
    uint256 constant IC1y = 9045718617374033938334534148199950652277581363725131126977514795832489383597;
    
    uint256 constant IC2x = 7940035212217149489091346041223742733332700278746355412134158794768275581053;
    uint256 constant IC2y = 2615144925918320500366689068819061138649445255385146685020394785891745898436;
    
 
    // Memory data
    uint16 constant pVk = 0;
    uint16 constant pPairing = 128;

    uint16 constant pLastMem = 896;

    function verifyProof(uint[2] calldata _pA, uint[2][2] calldata _pB, uint[2] calldata _pC, uint[2] calldata _pubSignals) public view returns (bool) {
        assembly {
            function checkField(v) {
                if iszero(lt(v, q)) {
                    mstore(0, 0)
                    return(0, 0x20)
                }
            }
            
            // G1 function to multiply a G1 value(x,y) to value in an address
            function g1_mulAccC(pR, x, y, s) {
                let success
                let mIn := mload(0x40)
                mstore(mIn, x)
                mstore(add(mIn, 32), y)
                mstore(add(mIn, 64), s)

                success := staticcall(sub(gas(), 2000), 7, mIn, 96, mIn, 64)

                if iszero(success) {
                    mstore(0, 0)
                    return(0, 0x20)
                }

                mstore(add(mIn, 64), mload(pR))
                mstore(add(mIn, 96), mload(add(pR, 32)))

                success := staticcall(sub(gas(), 2000), 6, mIn, 128, pR, 64)

                if iszero(success) {
                    mstore(0, 0)
                    return(0, 0x20)
                }
            }

            function checkPairing(pA, pB, pC, pubSignals, pMem) -> isOk {
                let _pPairing := add(pMem, pPairing)
                let _pVk := add(pMem, pVk)

                mstore(_pVk, IC0x)
                mstore(add(_pVk, 32), IC0y)

                // Compute the linear combination vk_x
                
                g1_mulAccC(_pVk, IC1x, IC1y, calldataload(add(pubSignals, 0)))
                
                g1_mulAccC(_pVk, IC2x, IC2y, calldataload(add(pubSignals, 32)))
                

                // -A
                mstore(_pPairing, calldataload(pA))
                mstore(add(_pPairing, 32), mod(sub(q, calldataload(add(pA, 32))), q))

                // B
                mstore(add(_pPairing, 64), calldataload(pB))
                mstore(add(_pPairing, 96), calldataload(add(pB, 32)))
                mstore(add(_pPairing, 128), calldataload(add(pB, 64)))
                mstore(add(_pPairing, 160), calldataload(add(pB, 96)))

                // alpha1
                mstore(add(_pPairing, 192), alphax)
                mstore(add(_pPairing, 224), alphay)

                // beta2
                mstore(add(_pPairing, 256), betax1)
                mstore(add(_pPairing, 288), betax2)
                mstore(add(_pPairing, 320), betay1)
                mstore(add(_pPairing, 352), betay2)

                // vk_x
                mstore(add(_pPairing, 384), mload(add(pMem, pVk)))
                mstore(add(_pPairing, 416), mload(add(pMem, add(pVk, 32))))


                // gamma2
                mstore(add(_pPairing, 448), gammax1)
                mstore(add(_pPairing, 480), gammax2)
                mstore(add(_pPairing, 512), gammay1)
                mstore(add(_pPairing, 544), gammay2)

                // C
                mstore(add(_pPairing, 576), calldataload(pC))
                mstore(add(_pPairing, 608), calldataload(add(pC, 32)))

                // delta2
                mstore(add(_pPairing, 640), deltax1)
                mstore(add(_pPairing, 672), deltax2)
                mstore(add(_pPairing, 704), deltay1)
                mstore(add(_pPairing, 736), deltay2)


                let success := staticcall(sub(gas(), 2000), 8, _pPairing, 768, _pPairing, 0x20)

                isOk := and(success, mload(_pPairing))
            }

            let pMem := mload(0x40)
            mstore(0x40, add(pMem, pLastMem))

            // Validate that all evaluations ∈ F
            
            checkField(calldataload(add(_pubSignals, 0)))
            
            checkField(calldataload(add(_pubSignals, 32)))
            
            checkField(calldataload(add(_pubSignals, 64)))
            

            // Validate all evaluations
            let isValid := checkPairing(_pA, _pB, _pC, _pubSignals, pMem)

            mstore(0, isValid)
             return(0, 0x20)
         }
     }
 }

I will update this post in future. Let me know what you think about this.

Cheers!!!